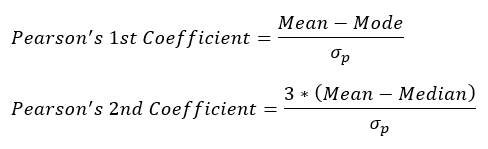Skewness is used to describe the distribution of a dataset. Provides a measure of the variance of a dataset relative to a Normal Distribution (i.e. where all data is symmetric and distributely equally around the mean). A dataset is skewed if the points are not symmetrical, for example, positive skew occurs if the right tail of the distribution is longer than the left. A symmetrical distribution will have 0 skewness.
Skewness and Kurtosis often go hand-in-hand as measures of describing a distribution. Skewness is calculated using Pearson Coefficients; these are 2 correlation coefficients whereby -1/+1 reflect perfectly negative/positive relationships and 0 represents no relationship. Pearson’s first coefficient uses the Mode and is calculated as: (Mean – Mode)/St Dev. Pearson’s second coeffient uses the Median and is calculated as: (3*(Mean – Median))/St Dev.