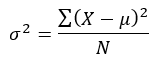Standard Deviation is a key measure of risk and volatility. It measures the volatility of an asset’s price movements relative to its mean. The more varied, or dispersed, the data, the greater the standard deviation.

Standard Deviation is simply calculated as the square root of Variance; the calculation for Variance is explained below.

For Downside Deviation we repeat the process but exclude any positive movements in the data, as these are not considered as a “risk”.

Variance is calculated in steps. These steps are as follows:

1. Calculate the data mean;
2. Calculate the residuals. Residuals are the difference between the observed data and the mean;
3. Square the residuals;
4. Sum the square of the residuals;
5. Divide by n-1, where n represents the number of observations.

Standard Deviation is then calculated simply as the square root of the variance.